Sabtu, 03 April 2010

momen inersia

(Skalar) momen inersia bagi jisim titik yang berputar pada paksi yang diketahui ditakrifkan sebagai

I \ \stackrel{\mathrm{def}}{=}\ m r^2\,\!

iaitu

m ialah jisim,
r is jarak (berserenjang) dari jisim titik ke paksi putaran.

Momen inersia adalah hasil campuran. Maka, bagi satu jasad tegar yang mengandungi N jisim titik mi dengan jarak ri ke paksi putaran, jumlah momen inersia adalah bersamaan jumlah momen inersia bagi jisim titik:

I \ \stackrel{\mathrm{def}}{=}\ \sum_{i=1}^{N} {m_{i} r_{i}^2}\,\!

Bagi jasad pejal yang ditakifkan sebagai fungsi ketumpatan jisim selanjar ρ(x,y,z), momen inersia pada paksi yang diketahui boleh diketahui dengan mengamirkan kuasa dua bagi jarak (yang diberatkan dengan ketumpatan jisim) dari titik dalam jasad ke paksi putaran:

I \ \stackrel{\mathrm{def}}{=}\ \iiint_V r^2 \,\rho(x,y,z)\,dx\,dy\,dz \!

iaitu

V ialah isi padu yang diisi objek. (Manakala kamiran tigaan mungkin boleh digunakan bagi semua ruang, hanya kawasan ρ(x,y,z) ≠ 0 yang menyumbang).
ρ ialah fungsi ketumpatan ruang bagi objek, dan
x, y, z adalah koordinat cartesian bagi satu titik dalam jasad.
Rajah bagi pengiraan momen inersia bagi cakera. Di sini, k adalah 1/2 dan r adalah jejari yang digunakan untuk menentukan momen.

Momen inersia bagi banyak objek bukan titik juga boleh ditakrifkan atau dianggarkan sebagai hasil darab tiga sebutan:

I \approx k\cdot M\cdot {R}^2 \,\!

iaitu

k ialah pemalar inersia,
M ialah jisim, dan
R ialah jejari objek dari pusat jisim (dalam sesetengah kes, panjang objek digunakan.)

Pemalar inersia digunakan untuk mengambil kira perbezaan dalam kedudukan jisim dari pusat putaran. Contoh termasuklah:

  • k = 1, cincin nipis atau silinder berdinding nipis sekitar pusatnya,
  • k = 2/5, sfera padu sekitar pusatnya,
  • k = 1/2, silinder padu atau cakera sekitar pusatnya.

Untuk contoh lain, sila lihat Senarai momen inersia.

[sunting] Persamaan melibatkan momen inersia

Tenaga kinetik putaran bagi sesuatu sistem boleh ditakrifkan sebagai sebutan momen inersia. Bagi sistem dengan N jisim titik mi yang bergerak dengan kelajuan vi, tenaga kinetik puataran T bersamaan dengan

T = \sum_{i=1}^{N} \frac{1}{2} m_{i} v_{i}^{2}\,\! = \sum_{i=1}^{N} \frac{1}{2} m_{i} (\omega r_{i})^{2} = \frac{1}{2} \sum_{i=1}^{N} m_{i} r_{i}^{2} \omega^{2} = \frac{1}{2} I \omega^{2}

iaitu ω adalah halaju sudut (dalam radian per saat). Rumus akhir T=\frac{1}{2} I \omega^{2}\,\! juga berguna untuk sebaran selanjar bagi jisim dengan pemerihalan umum bagi terbitan di atas dari jumlah diskret kepada pengkamiran.

Dalam kes khas iaitu vektor momentum sudut selari dengan vektor halaju sudut, maka boleh dikaitkan dengan persamaan

L = I\omega \;

iaitu L adalah momentum sudut dan ω adalah halaju sudut. Walau bagaimanapun, persamaan ini tidak digunakan untuk kebanyakan kes, seperti liukan bebas tork bagi objek berputar, walaupun bentuk tensor amnya selalunya betul.

Apabila momen inersia adalah malar, kita boleh kaitkan tork bagi sesuatu objek itu dengan pecutan sudut dalam persamaan yang serupa:

N = I\alpha \!

iaitu N adalah tork dan α adalah pecutan sudut.

Diposting oleh di

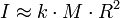
Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)